要啥和差化积，本质比技巧重要——2025年高考数学第19题深度研究

高考命题的悄然转向：从技巧演练到本质理解

高考已经过去六个多月，高一的同学不知不觉也学到了三角函数模块。从弧度制、同角三角函数关系，到诱导公式、二倍角公式，一步步搭建起三角知识的框架。最近重新审视2025年高考数学第19题这道三角压轴题，不再是当时追求快速破题的急切，反而有了新的感悟：这道题根本不是“超纲难题”，而是检验三角函数本质理解的绝佳范本——它真正要考的，从来不是和差化积这种“技巧性公式”，而是贯穿整个函数思想最本质的体现。

让我们先完整地看看这道题：

从表面上看，这是一道标准的三角函数综合题。但当我们剥开层层外壳，会发现它揭示的数学思想远比我们想象的要深刻。

第一问：回归导数本源，理解函数变化

第一问要求函数在特定区间的最值。最自然的思路是求导：

（1）解： $f'(x) = -5\sin x + 5\sin 5x$ 令 $f'(x) = 0$，即 $\sin x = \sin 5x$。 解得：$5x = x + 2k\pi$ 或 $5x = \pi - x + 2k\pi \ (k \in \mathbb{Z})$。 结合 $x \in \left[0, \frac{\pi}{4}\right]$，解得 $x = \frac{\pi}{6}$。

在区间 $\left[0, \frac{\pi}{6}\right)$ 上，$f'(x) > 0$，$f(x)$ 单调递增；在区间 $\left(\frac{\pi}{6}, \frac{\pi}{4}\right]$ 上，$f'(x) < 0$，$f(x)$ 单调递减。

因此 $f(x)$ 的最大值为： $f(x)_{\text{max}} = f\left(\frac{\pi}{6}\right) = 3\sqrt{3}$

本质思考：根本不需要和差化积！

这个简单的求解过程背后，隐藏着重要的数学思想：

三角方程的本质：两个角的正弦值相等，不是机械地套用公式，而是理解它们的几何意义——在单位圆上，这两个角要么对应同一个纵坐标（相差周期整数倍），要么关于y轴对称。

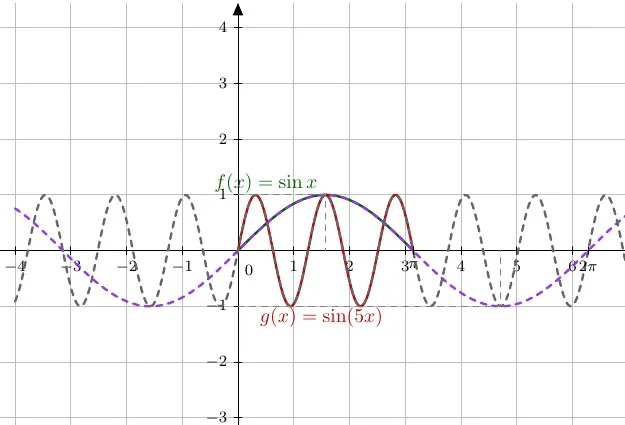
单调性的直观理解：在 $[0, \frac{\pi}{6})$ 上 $f'(x) > 0$，不是通过复杂的三角变换判断，而是理解 $\sin 5x$ 的变化速度比 $\sin x$ 快5倍，当 $x$ 很小时，$\sin 5x$ 增长更快。

函数图象的预测能力：有经验的学生应该能预测到这个函数的大致形态——一个高频振动叠加在低频振动上，形成"拍频"现象。这种物理直观在数学学习中同样重要。

为了下一步研究：将第一小问继续拓展研究：

进一步研究 $f(x)$ 的图象 $f(x)$ 的周期 $T = 2\pi$，且是偶函数。 在 $[0, \pi]$ 内，$f'(x) = 0$ 的解依次为 $\frac{\pi}{6}, \frac{\pi}{2}, \frac{5\pi}{6}$。

$f(x)$ 在 $[0, \pi]$ 上的单调性与极值表

区间	$\left[0, \frac{\pi}{6}\right)$	$x = \frac{\pi}{6}$	$\left(\frac{\pi}{6}, \frac{\pi}{2}\right)$	$x = \frac{\pi}{2}$	$\left(\frac{\pi}{2}, \frac{5\pi}{6}\right)$	$x = \frac{5\pi}{6}$	$\left(\frac{5\pi}{6}, \pi\right]$
$f'(x)$ 符号	$> 0$	$= 0$	$< 0$	$= 0$	$< 0$	$= 0$	$> 0$
$f(x)$ 单调性	单调递增	-	单调递减	-	单调递减	-	单调递增
极值类型	-	极大值点	-		-	极小值点	-
极值	-	$3\sqrt{3}$	-		-	$-3\sqrt{3}$	-

画出图像

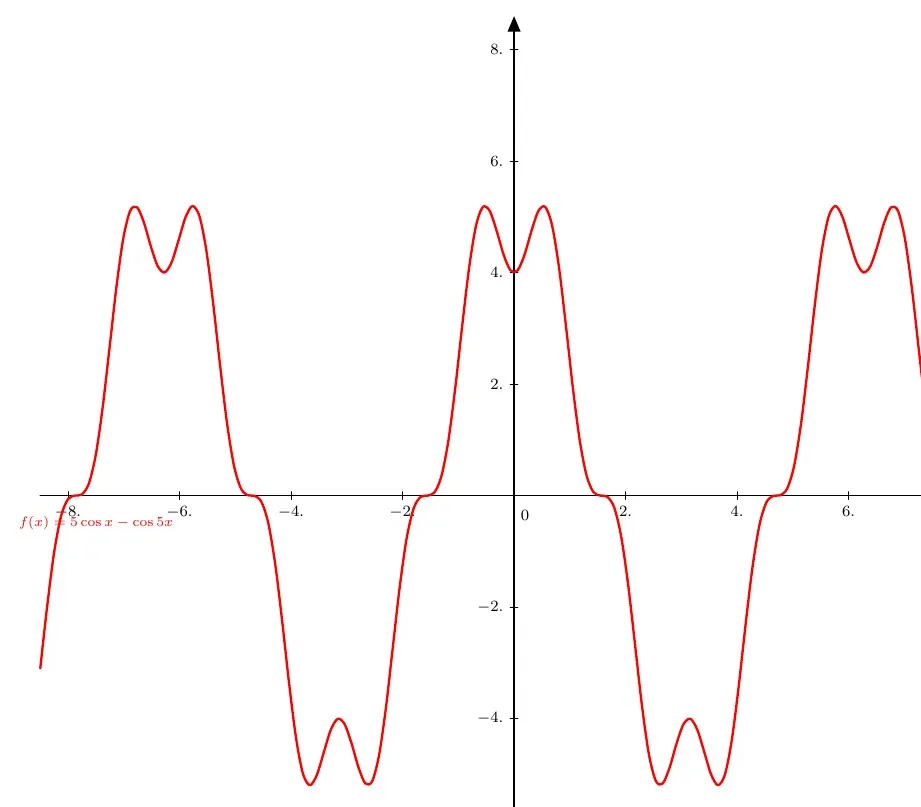
第二问：从晦涩语言到数学本质的翻译

命题语言的"数学翻译"

第二问的表述看似晦涩："给定 $\theta \in (0, \pi)$，设 $a$ 为实数，证明：存在 $y \in [a-\theta, a+\theta]$，使得 $\cos y \leq \cos \theta$"

翻译成大白话就是：求证：无论起点 $a$ 在数轴的哪个位置，对于一个给定的角度 $\theta$，在从 $a-\theta$ 到 $a+\theta$ 这个长度为 $2\theta$ 的区间内，总存在至少一个数 $y$，使得它的余弦值不超过 $\cos \theta$。

再进一步翻译成图像语言：在余弦函数的波浪线上，任意截取一段长度为 $2\theta$ 的片段，这个片段不可能完全停留在水平线 $y = \cos \theta$ 的上方。

多种证明思路的对比

思路一：反证法（最本质的理解）

反证法：假设 $\forall y \in [a-\theta, a+\theta]$，都有 $\cos y > \cos \theta$。 必有 $y \in (2k\pi-\theta, 2k\pi+\theta) \ (k \in \mathbb{Z})$。这是无数个不连续的长度为2θ的开区间的并集，而$\lbrack a - \theta , a + \theta \rbrack$是一个长度为2θ的闭区间，不可能包含于前者。所以矛盾。

因此假设不成立，必然存在 $y \in [a-\theta, a+\theta]$，使得 $\cos y \leq \cos \theta$。

思路二：正面求解，也可以由区间 $[a-\theta, a+\theta]$这一段的图象的位置来构造存在性，

法二：证明如下：

由余弦函数的周期性（周期为 $2\pi$），只需考虑 $a \in [0, 2\pi)$，分两种情况讨论：

（1）$0 \le a < 2\theta$ 此时可得：$a+\theta > \theta>a-\theta$；

取区间 $J = (\theta, \min(a+\theta, \pi))$，注意到： 余弦函数在 $(0, \pi)$ 上单调递减，因此在 $J$ 上，必然存在 $y \in J$，使得 $\cos y < \cos \theta$。

即 $y\in [a-\theta, a+\theta]$，满足 $\cos y \le \cos \theta$。

（2）$2\theta \le a < 2\pi$ 此时可得： $a-\theta \in [θ, 2\pi-θ)$。

有$\cos(a-\theta) \le \cos \theta$。

取 $y = a-\theta$，则 $\cos y \le \cos \theta$。

综上，无论哪种情况，都存在 $y \in[a-\theta, a+\theta]$ 使得 $\cos y \le \cos \theta$。

值得一提的是Deepseek的证法，虽然不对，但是还是比较漂亮的，我补充了一下并受其启发得到解法二。

Deepseek解法完善版：

证明：设 $g(y)=\cos y-\cos\theta$，需证 $\exists\;y\in I,\;g(y)\le0$。

若 $g(a)=\cos a-\cos\theta\le0$，取 $y=a\in I$，得证。 若 $g(a)>0$，计算区间端点函数值之和： $\begin{aligned} g(a+\theta)+g(a-\theta)&=\left[\cos(a+\theta)-\cos\theta\right]+\left[\cos(a-\theta)-\cos\theta\right]\\ &=2\cos a\cos\theta-2\cos\theta\\ &=2\cos\theta(\cos a-1)\le0 \end{aligned}$ 当 $\theta \in (0，\frac{\pi}{2})$ 时成立

故 $g(a+\theta)$ 与 $g(a-\theta)$ 至少一个 $\le0$，取对应端点为 $y\in I$，得证。

当 $\theta \in (\frac{\pi}{2},\pi)$ 时 结合 $a \in [0,2\pi)$ 再分三种情况：

若 $0 < a < 2\pi - 2\theta$，则 $\theta < a+\theta < 2\pi - \theta$，由余弦函数单调性可得 $\cos(a+\theta) < \cos\theta$；

若 $2\pi - 2\theta < a \le \pi + \theta$，则 $a-\theta < \pi < 2\pi - \theta < a+\theta$，而 $\cos\pi = -1 < \cos\theta$；

若 $\pi + \theta < a < 2\pi$，则 $\pi < a-\theta < 2\pi - \theta$，由单调性可得 $\cos(a-\theta) < \cos\theta$。

综上所述，命题成立。

第二问的真正价值在于训练学生的数学翻译能力： 从自然语言到数学语言的翻译；从代数表述到几何直观的翻译；从具体问题到一般原理的翻译。

这正体现了新高考"重思维、轻技巧"的导向。

第三问：函数族的优化与波动的哲学

问题的物理类比

第三问可以看作一个波形叠加的最优控制问题： 主振动：$5\cos x$（振幅5，频率1） 控制振动：$-\cos(5x+\varphi)$（振幅-1，频率5，相位可调）

我们要通过调节相位 $\varphi$，让合成波形的最大振幅最小化。

第三问逻辑上是求max值的min值，当$\varphi=0$,同频共振，可以猜想此时最大值应该是最小的。其次是（2）问的解决看似与主线无关，但是高考题不会这样，这样就想用（2）问的结论去证明这个猜想。

解题的关键洞察：

当 $\varphi = 0$ 时，函数简化为第一问的 $f(x)$，最大值已知为 $3\sqrt{3}$

证明这是最优的：对任意 $\varphi \neq 0$，利用第二问的结论

由（2）可知，存在 $x \in \left[-\frac{\pi}{6}, \frac{\pi}{6}\right]$，使得 $5x+\varphi \in \left[\varphi-\frac{5\pi}{6}, \varphi+\frac{5\pi}{6}\right]$，进而 $\cos(5x+\varphi) \leq \cos \frac{5\pi}{6}=-\frac{\sqrt{3}}{2}$，此时$5cosx ≥ \frac{5\sqrt{3}}{2}$ 所以$h(x)_{max}≥ 3\sqrt{3}$，

综上，$b$ 的最小值为 $3\sqrt{3}$。

高考改革的深层信号：告别题海，回归数学

从"怎么做"到"为什么"

传统的高中数学教育往往强调"题型"和"技巧"： 看到三角函数求最值，就想"辅助角公式" 看到不等式证明，就想"均值不等式" 看到存在性问题，就想"构造函数"

但2025年的这道题告诉我们：机械的题型对应已经失效了。

新高考的四大导向

理解重于记忆：不需要背和差化积公式，但要理解三角函数的图像性质 思维重于技巧：不需要复杂的代数变形，但要有清晰的逻辑推理 联系重于孤立：三个小问环环相扣，前面为后面铺垫 应用重于形式：问题有明确的物理背景和实际意义

对教学的启示

对教师： 少讲"套路"，多讲"原理" 少做"偏题"，多做"典题" 少强调"速度"，多培养"深度"

对学生： 不要满足于"会做"，要追求"懂为什么" 不要死记"公式"，要理解"来源" 不要孤立"知识点"，要构建"知识网"

以下由deepseek生成：

数学之美的普遍性：从高考题到科学前沿

这道看似朴素的高考题，实际上揭示了数学中一些普遍而深刻的原理

周期函数的"覆盖定理" 第二问的本质可以推广为：对于任何连续的周期函数，给定一个水平线，函数值大于该水平线的区域由若干区间组成，每个区间的长度有限。因此，任何足够长的区间必然与该区域的补集相交。

这个原理在： 信号处理：保证在足够长的时间窗口内能检测到信号 控制系统：保证系统状态必然经过某些区域 金融数学：价格波动必然回归均值

多频振动的"相位优化"

第三问的本质是：通过调节多个振动的相对相位，使合成振动的峰值最小化。

这应用于： 结构工程：减小建筑物在风载下的振动 电子工程：降低电路的峰值功率 音乐合成：创造更和谐的声音

函数族的"包络分析" 整个问题涉及对函数族的整体分析，这通向： 泛函分析：函数空间的几何结构 优化理论：参数族的最优控制 动力系统：参数变化时的定性行为

生成结束。

写给正在学习三角函数的你

如果你现在是高一学生，正在学习三角函数，请记住：

不要被公式吓倒**。三角函数不是一堆需要死记硬背的公式，而是一个**描述周期性现象的自然语言。

重视图像直观。每一个三角公式都有其几何意义，画图理解比代数推导更本质。

理解变化规律。单调性、周期性、对称性——这些才是三角函数的灵魂。

建立联系网络。把三角函数与向量、复数、波动、旋转联系起来，形成整体认知。

高考改革的方向已经明确：减少技巧性，增加思维性；减少记忆性，增加理解性；减少孤立性，增加联系性。

2025年的这道题，就是这一改革的明确信号。它告诉我们：数学的本质不是解题技巧的堆砌，而是对世界规律的理解和描述。

当我们真正理解了数学的本质，就不再需要"题海战术"，因为万变不离其宗；当我们掌握了数学的思想，就不再害怕"新颖题型"，因为原理相通，思维相通。

要啥和差化积？我们要的是数学的本质。

这，才是高考想要选拔的人才——不是解题机器，而是思考者。