基于阅读提升和方法研究的试题研究

学习目标

理解教材中阅读素材的功能及价值，增强数学应用意识
从阅读材料的背景、数据中获取信息，对提炼出的数学知识进行分析、综合、归纳、推理、猜想，加深对数学知识本质的理解

教学重点与难点

教学重点

阅读信息的提炼，探究方法的归纳

教学难点

阅读方式的优化、引领本质的揭示、思想方法的迁移、数学模型的构建

一、教材回归

通过对人教版、苏教版教材中"阅读材料"与"问题探究"等课程资源的回顾，促进高三学生考前把教材作为重要学材使用的必要性。

流星不是地球蒸发物

仰望星空，时有流星到过天际。"流星，飞走天空，可能有一秒时的凝望，然而这一餐的光明，已长久遭留在人的心怀里"(引自冰心《繁星·春水》)人们赞美流星，是因为它燃烧着走完自己的全部路程。

流星是什么?自古以来人们做过无数种猜测。古希腊哲学家亚里士多德说，那是地球的蒸发物。后来还有人认为，流星是地球上的磷火升空后的燃烧现象。

10世纪阿拉伯天文学家阿尔·库希(al-Kuhl)设计出一种方案，通过两个观察者异地同时观测同一颗流星来测定流星的高度。18世纪与19世纪之交，德国天文学家本森伯格(J. Benzenberg, 1777-1846)和布兰第斯(H.W. Brandes, 1777-1834)独立采用同样的方法测定流星的高度。

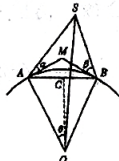
图2 流星观测示意图

如图2，设有两个观察者在地球上A,B两地同时观察到一颗波差S，仰角分别是a和β(MA, MB表示当地的地平线)。

由$\widehat{A B}$的长度$l$和地球的半径$R$，可求得$\widehat{A B}$所对的圆心角为$2\theta=\frac{l}{2\pi R}\times 360^{\circ}$，则$AB=2R\sin\theta$。在$\triangle SAB$中，$\angle SAB=\theta+\alpha$，$\angle SBA=\theta+\beta$，故由$AB$的大小可以求得$SA$；在$\triangle SAO$中，$\angle SAO=\angle OAM+\angle MAS=90^{\circ}+\alpha$，可求得$OS$，再减去地球半径$R$，就得到流星$S$的高度。

但是，阿尔·库希当时还不知道三角形的正弦定理，而关于余弦定理，中世纪的数学家只知道《原本》中的几何形式，因此他的方法非常繁琐。

阿拉伯学者阿布·瓦法(Abu'l-Wafa, 940-998)首先提出并证明了球面三角形的正弦定理，而平面三角形的正弦定理的证明最先是纳绥尔丁·图西(Nasir al-Din al-Tusi,1201-1274)给出的。《论四边形》被称为是纳绥尔丁最重要的数学论著，是数学史上流传至今最早的三角学专著，书中他明确陈述了正弦定理：

$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$

他的工作完成了球面三角和平面三角的系统化，使三角学脱离天文学而成为数学的独立分支。

有了余弦定理和正弦定理，我们可以方便地解决流星高度问题。

在图2中，设$\alpha=23.2^{\circ}$，$\beta=44.3^{\circ}$，$l=500\text{km}$，$R=6371\text{km}$，则：

$$\theta=\frac{1}{2}\times\frac{500}{2\pi R}\times 360^{\circ}\approx 2.2483^{\circ}$$

$$AB=2R\sin\theta\approx 499.8708\text{km}$$

在$\triangle SAB$中：$\angle SAB=\theta+\alpha=25.4483^{\circ}$，$\angle SBA=\theta+\beta=46.5483^{\circ}$，所以$\angle ASB=108.0034^{\circ}$。

由正弦定理$\frac{AB}{\sin\angle ASB}=\frac{AS}{\sin\angle SBA}$，得$AS\approx 381.5655\text{km}$。

在$\triangle SAO$中，$\angle SAO=90^{\circ}+\alpha=113.2^{\circ}$。

由余弦定理得：

$$OS=\sqrt{AS^2+R^2-2AS\cdot R\cos\angle SAO}\approx 6530.7382\text{km}$$

再减去地球半径，最后求出流星的高度为$h\approx 159.7382\text{km}$。

我们知道，云层最高不超过$15\text{km}$，所以可以断定流星不是地球蒸发物，它一定是天外来客！正是余弦定理和正弦定理帮助人们迈出正确认识流星的第一步！

二、学科比较

语文阅读是以文本为载体，通过分析、理解与鉴赏，提升语言运用、逻辑思维及审美能力的综合过程，涵盖文学、实用类及文言文等类型，旨在传承文化、塑造价值观，并为学术与人生奠基。

英语阅读是指通过语言符号与非语言符号(如图表、图片、标识等)共同构成的多模态文本，进行理解、分析、推理与评价的综合性语言活动，体现语言的交际性与文化性特征。英语阅读理解注重信息提取、推理判断、归纳概括能力，还重视对文章结构、语篇逻辑、作者意图及情感态度的深入理解。

数学阅读是从背景、数据等材料中获取信息的心理活动过程，不仅包括对数学文字语言、符号语言、图表语言的理解、记忆、认知等过程，还包括对材料的逻辑结构进行分析、综合、归纳、推理、猜想等一系列思维过程，是区别于一般阅读的较为复杂的智力活动。

通过对两门语言学科与数学学科阅读内涵与特征的比较，强调数学阅读是通过抽象概括、数据分析、推理运算、数学建模等一系列数学活动来理解材料所包含的数据、符号、图表、递推关系等，从而归纳出数量关系和空间形式的能力，是知识的重建过程。数学阅读是一个完整的心理活动过程，强调数学的逻辑性、结构性、抽象性等。

三、阅读研学

(2022年新高考I卷第4题)

南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库。已知该水库水位为海拔148.5m时，相应水面的面积为140.0km²；水位为海拔157.5m时，相应水面的面积为180.0km²，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m上升到157.5m时，增加的水量约为($\sqrt{7}\approx 2.65$)()

$$\text{A.}\quad 1.0\times 10^9 m^3$$ $$\text{B.}\quad 1.2\times 10^9 m^3$$ $$\text{C.}\quad 1.4\times 10^9 m^3$$ $$\text{D.}\quad 1.6\times 10^9 m^3$$

解析：根据棱台体积公式：

$$V = \frac{1}{3}h(S_1 + S_2 + \sqrt{S_1S_2})$$ $$= \frac{1}{3} \times 9 \times (140 + 180 + \sqrt{140 \times 180}) \times 10^6$$ $$\approx 3 \times (320 + 2.65 \times 158.75) \times 10^6$$ $$\approx 3 \times (320 + 420.7) \times 10^6$$ $$\approx 1.2 \times 10^9 m^3$$

因此正确答案是B。

(2023年新高考II卷第12题)

在信道内传输0,1信号，信号的传输相互独立。发送0时，收到1的概率为$\alpha(0<\alpha<1)$，收到0的概率为$1-\alpha$；发送1时，收到0的概率为$\beta(0<\beta<1)$，收到1的概率为$1-\beta$。考虑两种传输方案：单次传输和三次传输。单次传输是指每个信号只发送1次，三次传输是指每个信号重复发送3次。收到的信号需要译码，译码规则如下：单次传输时，收到的信号即为译码；三次传输时，收到的信号中出现次数多的即为译码(例如，若依次收到1,0,1，则译码为1)()。

A.采用单次传输方案，若依次发送1，0，1，则依次收到1，0，1的概率为$(1-\alpha)(1-\beta)^2$

B.采用三次传输方案，若发送1，则依次收到1，0，1的概率为$\beta(1-\beta)^2$

C.采用三次传输方案，若发送1，则译码为1的概率为$\beta(1-\beta)^2+(1-\beta)^3$

D.当$0<\alpha<0.5$时，若发送0，则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率

解析：

A选项：概率应为$(1-\beta)(1-\alpha)(1-\beta)$，不正确。

B选项：正确，因为每次传输独立，概率为$\beta(1-\beta)^2$。

C选项：译码为1的概率应包括所有收到2个或3个1的情况，表达式不完整。

D选项：三次传输译码为0的概率为$(1-\alpha)^3 + 3\alpha(1-\alpha)^2$，单次传输为$1-\alpha$，当$0<\alpha<0.5$时，前者确实大于后者。

因此正确答案是B、D。

(2021年新高考II卷第4题)

北斗三号全球卫星导航系统是我国航天事业的重要成果。在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km(轨道高度是指卫星到地球表面的距离)。将地球看作是一个球心为O，半径r为6400km的球，其上点A的纬度是指OA与赤道平面所成角的度数。地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α，记卫星信号覆盖地球表面的表面积为$S=2\pi r^2(1-\cos\alpha)$(单位：km²)，则S占地球表面积的百分比约为()。

$$\text{A.26\%}$$ $$\text{B.34\%}$$ $$\text{C.42\%}$$ $$\text{D.50\%}$$

解析：

根据几何关系，$\cos\alpha = \frac{r}{r+h} = \frac{6400}{6400+36000} \approx 0.151$

$$\frac{S}{4\pi r^2} = \frac{2\pi r^2(1-\cos\alpha)}{4\pi r^2} = \frac{1-\cos\alpha}{2} \approx \frac{1-0.151}{2} \approx 0.4245$$

即约42%，最接近的是C选项。

(2021年新高考I卷第16题)

某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为20dm×12dm的长方形纸，对折1次共可以得到$10dm×12dm$，$20dm×6dm$两种规格的图形，它们的面积之和$S_1=240dm^2$，对折2次共可以得到$5dm×12dm$，$10dm×6dm$，$20dm×3dm$三种规格的图形，它们的面积之和$S_2=180dm^2$，以此类推，则对折4次共可以得到不同规格图形的种数为______；如果对折n次，那么$\sum_{k=1}^n S_k=$______dm²。

解析：

对折1次：2种；对折2次：3种；对折3次：5种；对折4次：8种（斐波那契数列）。

面积和：

$$S_1 = 240 = 240 \times \left(\frac{1}{2^0} + \frac{1}{2^1}\right)$$ $$S_2 = 180 = 240 \times \left(\frac{1}{2^1} + \frac{1}{2^2}\right)$$ $$\vdots$$ $$\sum_{k=1}^n S_k = 240 \times \left(n + 2 - \frac{1}{2^{n-1}} - \frac{1}{2^n}\right)$$

因此对折4次有8种规格，$\sum_{k=1}^n S_k = 240 \times \left(3 - \frac{1}{2^{n-1}} - \frac{1}{2^n}\right)$。

(探究题)

设$N=2^n(n\in N^*, n\geq 2)$，将N个数$x_1, x_2,\ldots, x_N$依次放入编号为1,2,…,N的N个位置，得到排列$P_0=x_1x_2\cdots x_N$。将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前$\frac{N}{2}$和后$\frac{N}{2}$个位置，得到排列$P_1=x_1x_3\cdots x_{N-1}x_2x_4\cdots x_N$，将此操作称为C变换，将$P_1$分成两段，每段$\frac{N}{2}$个数，并对每段作C变换，得到$P_2$；当$2\leq i\leq n-2$时，将$P_1$分成$2^i$段，每段$\frac{N}{2^i}$个数，并对每段C变换，得到$P_{i+1}$，例如，当$N=8$时，$P_2=x_1x_5x_3x_7x_2x_6x_4x_8$，此时$x_7$位于$P_2$中的第4个位置。

(1)当$N=16$时，$x_7$位于$P_2$中的第______个位置；

(2)当$N=2^n(n\geq 8)$时，$x_{173}$位于$P_4$中的第______个位置。

解析：

(1)对于$N=16$，$P_1$将奇数位和偶数位分开：

$P_1 = x_1x_3x_5x_7x_9x_{11}x_{13}x_{15}x_2x_4x_6x_8x_{10}x_{12}x_{14}x_{16}$

$P_2$对前8个和后8个分别进行C变换：

$P_2 = x_1x_5x_9x_{13}x_3x_7x_{11}x_{15}x_2x_6x_{10}x_{14}x_4x_8x_{12}x_{16}$

$x_7$位于第6个位置。

(2)对于$N=2^n$，$x_{173}$的位置可以通过二进制分析：

173的二进制是10101101，反转后是10110101，即181。

因此$x_{173}$在$P_4$中的位置是181。

四、课堂小结

数学阅读是通过抽象概括、数据分析、推理运算、数学建模等一系列数学活动来理解材料所包含的数据、符号、图表、递推关系等。
数学阅读强调数学的逻辑性、结构性、抽象性等特点。
通过实际问题理解数学概念和方法的应用价值。
掌握从生活语言到数学语言的转换能力。