四、教学过程
(一)课程导入(3分钟)
"同学们,在之前的立体几何学习中,我们遇到过各种各样的问题,比如证明线面平行、求线面角、二面角等。大家回想一下,我们常用哪些方法来解决这些问题呢?"
设计意图:通过提问,引导学生回顾已学知识,引发学生对立体几何解题方法的思考,为后续课程中对不同方法的比较与选择做铺垫,同时活跃课堂气氛,激发学生的学习兴趣。
(二)典例探究(20分钟)
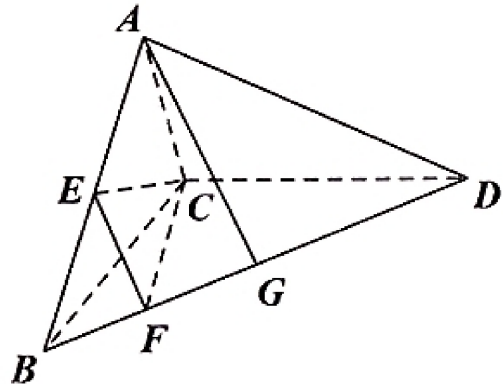
图1:四面体ABCD问题图示
"同学们,拿到这个题目,大家先思考一下,从题目所给的条件中,我们能获取哪些关键信息呢?对于第一个问题,要证明线面平行,我们有哪些常用的方法?对于第二个问题,求线面角,又可以从哪些角度入手呢?"
方法展示
| 方法 | 关键步骤 | 运算量 | 适用条件 |
|---|---|---|---|
| 坐标法 |
1. 以CH⊥CG建系 2. 利用∠AGC=30° 3. 计算各点坐标 4. 求法向量 |
★★★☆ | 存在三垂直关系 |
| 几何法 |
1. 构造CH⊥AG垂线 2. 解Rt△CEH 3. 利用线面角定义 |
★★☆☆ | 可确定摄影位置 |
| 基底法 |
1. 设GA,GB,GC为基底 2. 向量线性表示 3. 混合积运算 |
★★★★ | 向量关系明确 |
设计意图:通过具体数据对比,直观感受不同方法的复杂度差异,帮助学生理解不同方法的适用场景和优劣。
方法比较讨论
"在什么情况下,我们优先选择坐标法?什么情况下几何法更具优势?基底法适用于什么样的题目?"
图2:坐标法示意图(方式一)
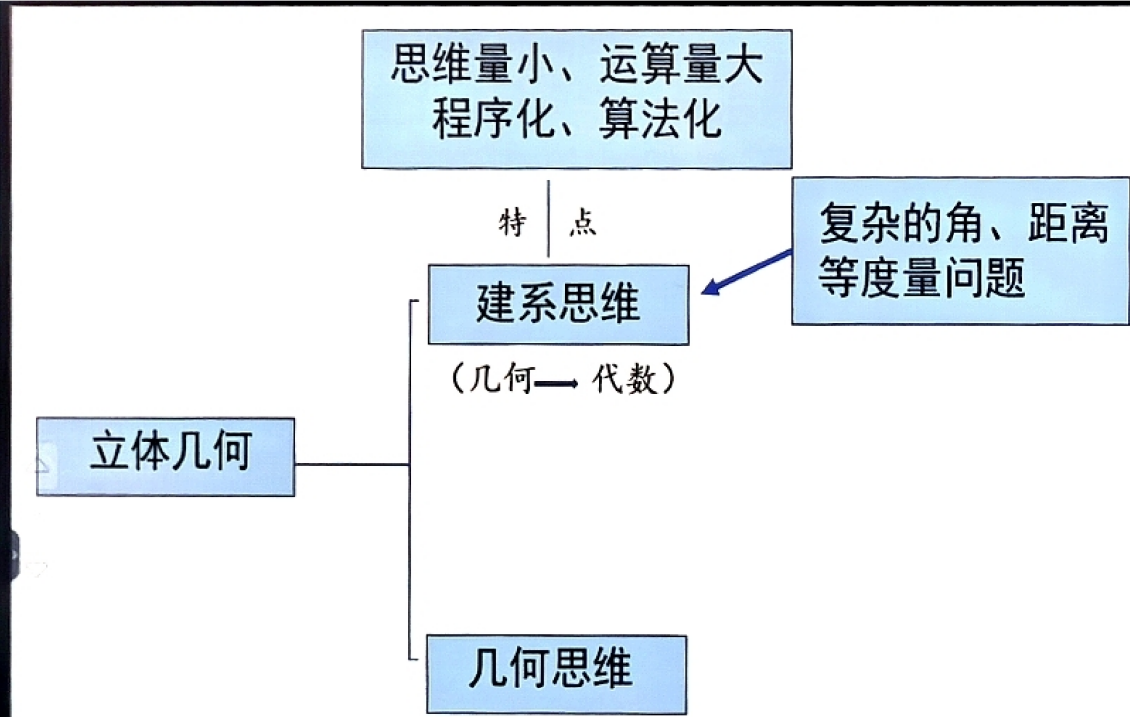
图3:几何法示意图
(三)真题回顾(15分钟)
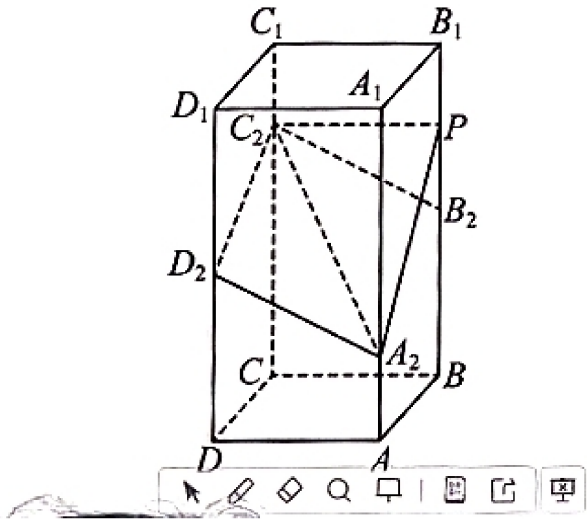
图4:2023新高考I卷第18题
多种证法展示
"看到这道真题,同学们先观察题目条件,思考一下证明线线平行可以用哪些方法?对于求二面角的问题,我们之前学习的方法在这里是否适用?"
向量法证明线线平行
以{CD, CB, CC₁}为正交基底,建立空间直角坐标系C-xyz,则:
A₂(2,2,1), B₂(0,2,2), C₂(0,0,3), D₂(2,0,2)
∴ B₂C₂ = A₂D₂ = (0,-2,1),又四点不共线,故B₂C₂∥A₂D₂
几何法证明线线平行
1. 在BB₁上取点E,使BE=1
2. 取CC₁中点F,连接A₂E, EF, FD₂
3. 证明四边形A₂D₂FE是平行四边形
4. 证明四边形C₂FEB₂是平行四边形
5. 由平行传递性得B₂C₂∥A₂D₂
设计意图:通过高考真题的解析,让学生了解不同方法在实际考试中的应用,提高学生的解题能力和应试技巧。
(四)感悟总结(5分钟)
"同学们,通过本节课的学习,大家对立体几何的解题方法有了更深入的理解。在今后的解题中,当遇到一个新的立体几何题目时,我们应该如何思考呢?"
方法选择策略:
- 坐标法:适用于规则几何体、动态轨迹问题、复杂度量计算
- 几何法:适用于对称图形分析、折叠展开问题、位置关系证明
- 基底法:适用于不规则图形、动态向量问题、难以建系情况
(五)当堂检测(7分钟)
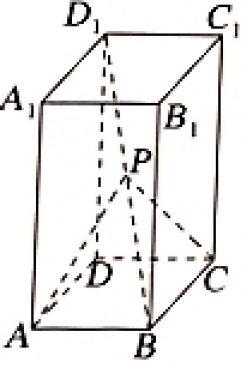
图5:当堂检测题(多选题)
"同学们,看到这些题目,大家先分析一下每个选项,思考可以用什么方法来解决。对于长方体中的动点问题,我们可以从哪些角度去考虑?对于直线旋转成角的问题,又该如何入手呢?"
(六)课堂小结(3分钟)
"世界上不变的唯一不变的就是变化,数学也是如此。所以同学们在解题时一定要冷静分析,理性判断,最后做出最佳选择。"
(七)布置作业
- 完成课本相关立体几何题目练习
- 分别用坐标法、几何法和基底法解答同一题目
- 比较不同方法的解题过程和优缺点