一题一课之法向量：定海神针破迷局

几何千面妙无穷，法向为针引道通。

距离角度藏妙算，空间万象纳心中。

几何图示

数学教研组 · 2025年

试题呈现

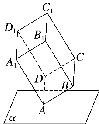
如图，长方体 $ABCD-A_1B_1C_1D_1$ 的顶点 A 在平面 $\alpha$ 内，其余顶点均在平面 $\alpha$ 的同侧，$AB=3$，$AD=4$，$AA_1=5$。

若顶点 B 到平面 $\alpha$ 的距离为 2，顶点 D 到平面 $\alpha$ 的距离为 2，求顶点 $A_1$ 到平面 $\alpha$ 的距离。

长方体图示
试题推荐

本题以长方体为基本图形，聚焦点到平面距离这一核心问题，兼具几何直观与代数运算的双重视角。

法向量作为平面的"代数基因"，承载了距离、角度等所有几何量的计算密码。其解题过程反套路化，无需复杂辅助线，仅通过条件直译、方程联立即可破局。

思维导图
解析过程
步骤一：建立坐标系

以 A 为原点，$AB$、$AD$、$AA_1$ 分别为 x、y、z 轴，得坐标：

$$ A(0,0,0),\ B(3,0,0),\ D(0,4,0),\ A_1(0,0,5) $$
步骤二：设平面法向量

设平面 $\alpha$ 的法向量为 $\vec{n}=(x,y,z)$，根据点到平面距离公式：

$$ \frac{|3x|}{\sqrt{x^2+y^2+z^2}}=2,\quad \frac{|4y|}{\sqrt{x^2+y^2+z^2}}=2 $$
步骤三：建立方程组

平方后整理得方程组：

$$ \begin{cases} 9x^2=4(x^2+y^2+z^2) & \Rightarrow 5x^2=4y^2+4z^2 \quad (1) \\ 16y^2=4(x^2+y^2+z^2) & \Rightarrow 3y^2=x^2+z^2 \quad (2) \end{cases} $$
步骤四：求解法向量

取 $x=2$，代入方程组得：

$$ y=\frac{3}{2},\quad z=\frac{\sqrt{11}}{2} $$

即法向量 $\vec{n}=\left(2,\frac{3}{2},\frac{\sqrt{11}}{2}\right)$

最终答案

顶点 $A_1$ 到平面 $\alpha$ 的距离为：

$$ d=\frac{|0\cdot x+0\cdot y+5z|}{|\vec{n}|}=\frac{5\cdot\frac{\sqrt{11}}{2}}{\sqrt{2^2+\left(\frac{3}{2}\right)^2+\left(\frac{\sqrt{11}}{2}\right)^2}}=\boxed{\dfrac{5\sqrt{11}}{6}} $$
解题思路

1. 建立适当坐标系，确定各点坐标

2. 设平面法向量，利用距离条件建立方程

3. 通过赋值法简化求解法向量

4. 代入距离公式计算最终结果

拓展延伸
拓展1：求 $C_1$ 到平面 $\alpha$ 的距离

$C_1$ 坐标为 $(3,4,5)$，向量 $\overrightarrow{AC_1}=(3,4,5)$

$$ d=\frac{|3x+4y+5z|}{|\vec{n}|}=\frac{|3\cdot2+4\cdot\frac{3}{2}+5\cdot\frac{\sqrt{11}}{2}|}{3}=\frac{12+\frac{5\sqrt{11}}{2}}{3}=\boxed{\dfrac{5\sqrt{11}}{6}+2} $$
拓展2：求 $A_1A$ 与平面 $\alpha$ 所成角

直线 $A_1A$ 的方向向量为 $\vec{v}=(0,0,-5)$

$$ \sin\theta=\frac{|\vec{v}\cdot\vec{n}|}{|\vec{v}|\cdot|\vec{n}|}=\frac{|5z|}{5\cdot|\vec{n}|}=\frac{\sqrt{11}}{6} $$

故 $\sin\theta=\boxed{\dfrac{\sqrt{11}}{6}}$

拓展3：求侧面与平面 $\alpha$ 所成的角

侧面 $ABB_1A_1$ 的法向量为 $\vec{n_1}=(0,1,0)$

$$ \cos\varphi=\frac{|\vec{n}\cdot\vec{n}_1|}{|\vec{n}|\cdot|\vec{n}_1|}=\frac{\frac{3}{2}}{3}=\frac{1}{2} $$

故 $\cos\varphi=\boxed{\dfrac{1}{2}}$

方法总结
定海神针妙解

1. 法向量本质：平面的"定海神针"，凝聚距离、角度等几何量的关键参数

2. 条件转化：将点到平面的距离转化为法向量与向量的点积绝对值之比

3. 方程思想：通过距离条件建立方程组，赋值简化求解

4. 通法迁移：适用于线面角、面面角、点面距离等立体几何核心问题

法向量如定海神针，穿云破雾，在空间几何中勾连起距离与角度的奥秘。

掌握其核心，便能以不变应万变，于方寸之间见天地。